Hardy's theorem

In mathematics, Hardy's theorem is a result in complex analysis describing the behavior of holomorphic functions.

Let $f$ be a holomorphic function on the open ball centered at zero and radius $R$ in the complex plane, and assume that $f$ is not a constant function. If one defines

$I(r) = \frac{1}{2\pi} \int_0^{2\pi}\! \left| f(r e^{i\theta}) \right| \,d\theta$

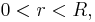for $0< r < R,$ then this function is strictly increasing and logarithmically convex.

References

John B. Conway. (1978) Functions of One Complex Variable I. Springer-Verlag, New York, New York.

This article incorporates material from Hardy's theorem on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.

Hardy's theorem

See also

References